Column buckling is a very unique subject and deserves more of your attention. Column buckling is the only area of mechanics where there’s a different outcome. It starts with predicting how much weight the column can hold and seeing if it can support any more.
In the 19th century, a number of columns were used to uphold the platform of new railway stations. When trains came in and left, the vibrations in the columns began to cause problems. Engineers soon found out that if a column is subjected to compression forces, it begins to buckle and as this process continues, it will eventually buckle all way around.
What Is Buckling?
Deformation in columns when axial load (i.e., compressive) is applied, or we can say that structural member or building elements which don’t support a provided load and experiencee a at once change in its configuration(shape) it is called buckling.
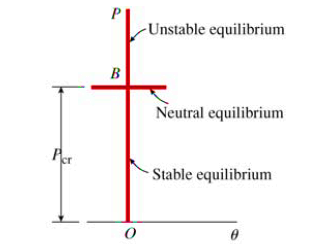
To understand buckling we have to understand stages of equilibrium (stability). There are three stages of equilibrium.
Unstable equilibrium
Unstable equilibrium is that when small disturbance (perturbation) is produced it causes large movements and structure never returns back to its original positions, as illustrated in below figure.
Neutral equilibrium
Neutral equilibrium is that in when it is no possible to decide for the structure whether it is in unstable or stable equilibrium. When a very little disturbances produce it will cause large movements but structure may be brought back to previous position (original) with no work done.

Stable Equilibrium
In stable equilibrium, structure with small disturbance (perturbation) don’t produce large movements, and structure return to original position as soon as disturbance remove. There are two main reasons when equilibrium state becomes unstable due to.
- Large deformations of the structure
- elasticity of the structural materials
So, the definition of stability had no relation as the geometry of structure under the effect of compressive force. Buckling is an effect which be occur under the effect of compressive load for structure.
Buckling and Structural Member
Long or slender column is aa line element which is subjected to compressive load. Buckling is may be in slender column (long column) and in web of beams like channel section, I section etc. Structural members (i.e., beams) may behave as stable structure when tensile loading is subjected to them, they may fail the stress are more the its ultimate strength.
In matter of elements (i.e., column) when it has compressive force, bending effects(secondary) like imperfection in the provided materials or may be in the process of fabrication, eccentric loading which is inaccurate placement of loads, unsymmetrical cross section can cause premature column failure which may be local or global. In this matter failure is bulking.
Types Of Buckling
Here are some types of buckling.
- Overall buckling
- Distortional Buckling
- Lateral Torsional buckling
- Torsional Flexural Buckling
- Global Buckling
- Local buckling
- Flexural Buckling
Overall Buckling
compressive members design is mostly affected by based on overall buckling capacity. Like the compressive load which is maximin can be carried before the buckling is due to much buckling in the plane of highest slenderness. Mostly overall buckling in case occurs in column of frame structure and in member of compressive load.
Distortional Buckling
Distortional buckling for the most part occurs for nearly more smaller beams. This is the final product of an exchange between the 2 types of buckling modes. Local buckling and lateral-twist buckling, the two of which are for the most part planned (designee) independently. While distortional buckling happens when the web is disfigured and the flanges turn (twist) and because of this it ends in deflection, the outcome being a low torsional resistance.
Lateral Torsional Buckling
When the axial load i.e., compression is applied on the structure members having small torsional stiffens may having great chances of buckling in such a way that its cross section is twisted. It is called Lateral Torsional buckling.
Torsional Flexural Buckling
This type of buckling mostly occur in beam of I section, channel section having monosymmetric system. At the point when it buckles the structural beam, it will bend together and consequently deflects. At the point when a pure bending moment follows up on an I-beam about its significant (major) axis, one flange of beam goes through compression and the other goes through tension.
Global Buckling
This type of buckling happens globally and impacts the beam is known as globally buckling. Global Buckling can be similarly subdivided relying on the kind of load appearing on the beam and kind of deformation that takes place.
Local Buckling
In this axis of structural member does not change, because it happens on a specific part of Colum or web of beams, but the strength beam or column cross section is reduced by the buckling of a component of that structural member.
Flexural Buckling
A beam can buckle in a plane without twisting is called flexural buckling. which may be under moment, axial or simultaneously loading condition. On the off chance that a part of member goes through pure axial load, it might twist in lateral direction and take the state of a sinus wave.
The quantity of waves can fluctuate and is reliant upon end conditions and side (lateral) limitations. This sort of is likewise called the Euler buckling case.
Also Read: Shear Wall Types and Design Techniques for Shear Wall
Causes of Buckling
The following factors that cause buckling:
Yielding
Exorbitant yielding and buckling of reinforcement happen in seriously harmed concrete member i.e., beam and columns. The reinforcement may furthermore have buckled, extended or unreasonably yielded in such members.
The reasons for buckling and yielding of steel in substantial designs happen because of surprising use of burdens for which the part was not designed or because of durability issues in concrete.
Eccentric Loading
Inquisitively, the mechanics of eccentric (loaded) column buckling can be seen additional straight-forward than these of the old-style hypothesis. For, dislike traditional failure of column buckling right here can related to material’s yield strength certainly.
As a matter of fact, it will be demonstrated that underneath conditions like eccentric loading, failure will consistently appear because of stresses surpassing the material’s yield power sooner than the load arrives at its so-called critical value.
Erosion
On the off chance that a substantial design isn’t safeguarded from the erosive impacts of the components, for example, water and acids, its structure integrity respectability could be compromised, making the whole construction causes buckling and failed.
This happens in regions like foundation and basement, where unnecessary water or dampness gathers. Salt water is especially risky to substantial structures since it can likewise causes rusting the reinforcement inside the concrete structure.
Compressive Stress
Concrete is especially impervious to compressive or vertical burdens, which is the reason it is utilized generally in footings and foundation. Nevertheless, on the off chance that the load acting on a concrete structure is more then the design load (also called critical load) it will make the structure to buckle under the weight.
The critical load is determined by its cross-section, the elasticity of the materials that make it and the region over which the force is conveyed for the concrete structure or column.
Lateral Forces
Concrete might be great at enduring vertical loads yet it is relatively defenseless against lateral loads. To that end concrete designs are frequently supported with steel (reinforce concrete), which has integral attributes, less strength on vertical burdens, stronger on lateral forces.
On the off chance that a concrete design structure gets an additional sideway or horizontal forces, it could buckle. This happens frequently during quakes, which incur greater lateral forces on structure.
Change In Heat
During winter and summer material expend and contract. For that reason, engineer’s configuration concrete designs with development joints that permit the construction to extend and contract without buckling.
Be that as it may, on the off chance that expansion joints are not embedded, or on the other hand assuming that these extension joints get filled in with unfamiliar material, it could make the concrete structure design buckle when the temperature increments. This frequently occurs with concrete clearing during the warm weather.
Column Buckling
SLENDERNESS RATIO (Le /rmin)
It is the length of column (effective, Le) to the minimum radius of gyration (rmin) of cross-sectional area, the ratio of both of these is called slenderness ration. Buckling will take palace where rmin (minimum radius f gyration) if the free rotation at end of column is allowed.
Slender Column
Buckling is mostly in slender or long column. Column is said to be long if ration of its effective length to its least dimension more than twelve (12) then column is said to be slender column. To describe a vertical member this term is frequently used, also its length is greater than least cross-sectional dimension (30 times).
Element of such types failed because of excess later deflection at value of stresses which are much less than the crushing value. Flexures stress are dominant in slender column then the compressive stress.
Euler’s Theory of Column Buckling
Euler’s hypothesis of buckling for column was created by Leonhard Euler a Swiss mathematician in 1757.Euler’s guideline of section buckling is utilized to gauge the basic buckling load of section as the stress in the section stays versatile. Euler’s thought is basically founded on certain suppositions referring to axial load application, cross-section, factor of column failure, column material and stress limit. Buckling failure happens when the size of the segment is expanded than its cross-area. Euler’s guideline expresses that the stress in the section because of a direct load is more modest than the stresses due to buckling failure.
Assumption
- Tension which is within the column are inside of elastic limit.
- Substances of the column are homogeneous and isotropic
- Initially, element (column) definitely straight.
- To its cross-sectional dimensions, size of the column is giant in evaluation.
- The far ends of the columns have no friction.
- The self-weight of the column itself is ignored.
- Column failure is solely due to buckling.
- Column cross sectional is even (uniform) all through its length.
- Axial load is passes through the centroid of the segment.
Euler’s Formula For Buckling
Pₑ = π²EI / le²
le = Effective length
Pₑ = Buckling load
I = Moment of inertia
E = Modulus of Elasticity
Effective length for critical buckling load
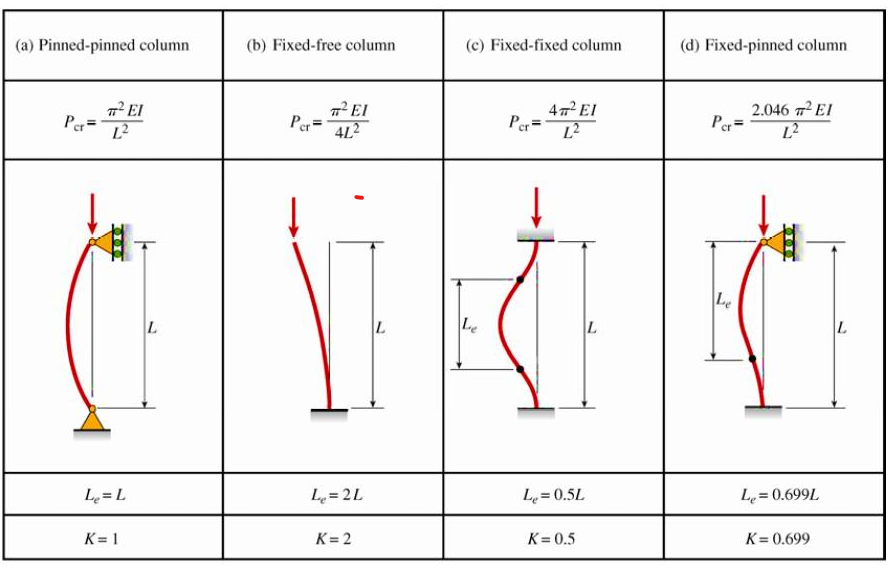
Effective Length (Le )
It is the length of the column corresponding to the half sigh wave or length between the point of contra-flexure. For fundamental buckling the Euler critical load depends upon the effective length.
Effective Length Factor (K)
Ratio between the effective length and original length. The Factor K depends upon the end/boundary Condition of the column.
Critical buckling load of column
The critical load of as slender bar (columns) subjected to axial compression is that value of the axial load that is just sufficient to keep the bar a slightly deflected configuration.
Case-I: P < Pcr Stable Equilibrium and No Buckling
Case-II: P = Pcr Equilibrium State and Slight deflection
Case-III: P > Pcr Unstable State and Buckling